index

The Gamma function $\Gamma(z)$ is essentially a continuous extension of the factorial function. It is defined for real numbers and complex numbers with the following formula:

$$\Gamma (z) = \int_0^\infty t^{z-1} e^{-t} \ \mathrm{d}t, \quad \Re(z) > 0$$

This construction of $\Gamma(z)$ converges for $\Re (z) > 0$, but it extends meromorphically elsewhere.

If $z$ is a positive integer (that is, $z \in \mathbb{N}^* = \{ 1,2, \ldots \}$) then $\Gamma(z) = (z-1)!$.

It is currently unknown if $\Gamma(\tfrac{1}{5})$ is irrational or transcendental. If it turned out to be rational, its decimal expansion would eventually fall into a repeating cycle. No such repetition has been found (much less proven), and many believe $\Gamma(\tfrac{1}{5})$ to most likely be transcendental.

Putting theory into practice

Using y-cruncher, I calculated 175 billion digits of Gamma(1/5) with this laptop in my dorm (window open for ventilation):

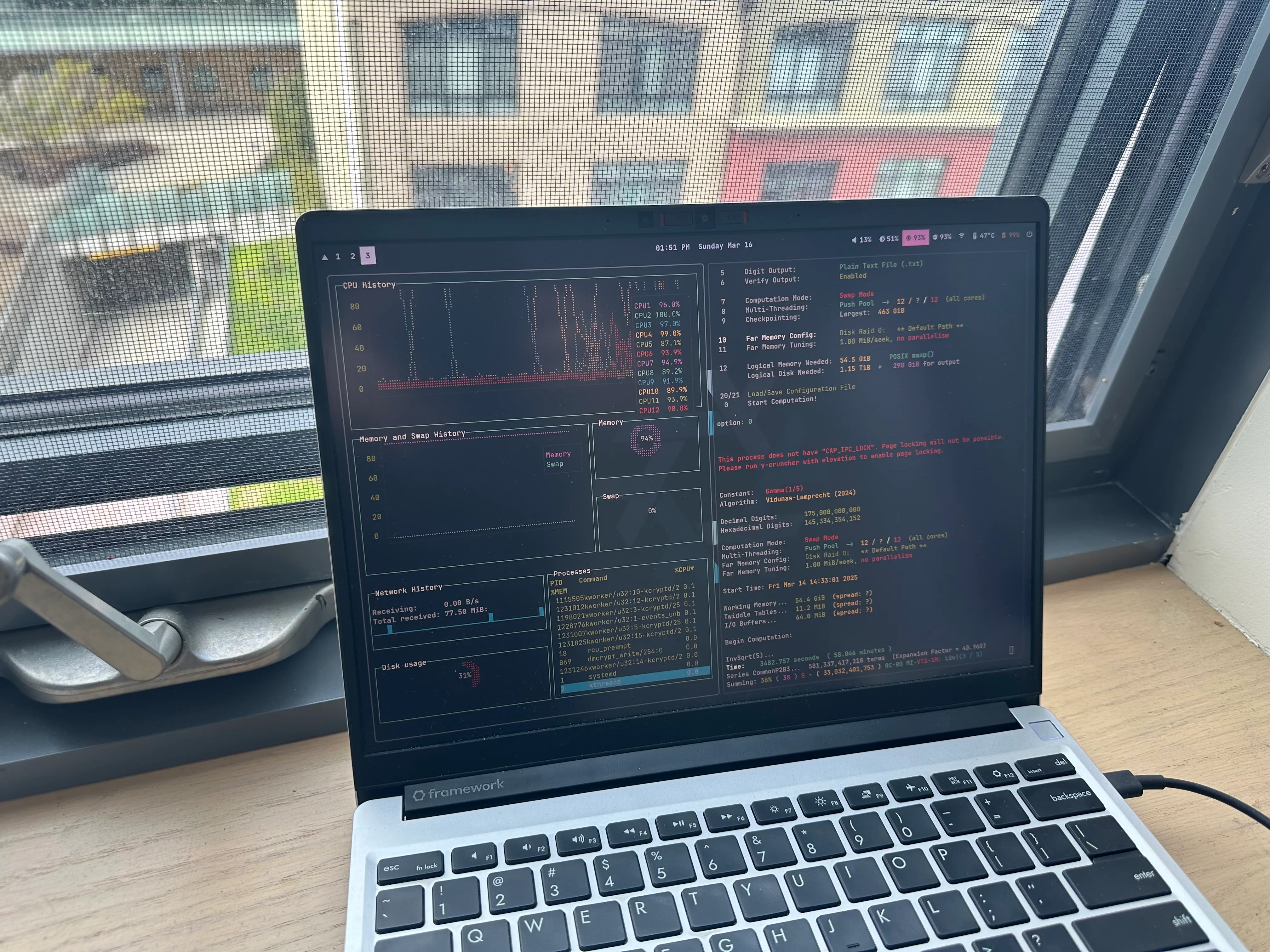
Component	Specification
Processor	AMD Ryzen 5 7640U
Topology	12 threads / 6 cores / 1 socket
Usable Memory	62.0 GiB
Usable Storage	1.14 TiB

I ran the calculation twice to verify my results:

The first calculation used the Vidunas-Lamprecht (2024) algorithm provided by y-cruncher and was run on a framework laptop running NixOS.

$$\Gamma( \tfrac{1}{5} ) = \frac{ \sqrt{5} }{ (\sqrt{5} + 5)^{(-1/10)} \cdot \pi^{(-1/5)} \cdot 2^{(-19/50)} \cdot H_1^{(-2/5)} \cdot H_2^{(-1/5)} }$$

where

$$H_1 = \int_0^1 \frac{ \mathrm{d}z }{ \sqrt{1-z^5} }, \quad H_2 = \int_0^1 \frac{z \ \mathrm{d}z}{ \sqrt{1-z^5} }$$

The second calculation used the Incomplete Gamma Approximation algorithm (also provided by y-cruncher) for verification and was run on a server running Debian in a Proxmox container. This method uses the lower incomplete gamma function (given below) to approximate $\Gamma (\tfrac{1}{5})$ to the desired precision.

$$\gamma (s,x) = \int_0^x t^{s-1} e^{-t} \ \mathrm{d}t$$

The results from these calculations matched perfectly, indicating that the computation was successful. Here are some interesting stats from these computations:

Method	Read	Written	Computation Time
VL	503 TiB	443 TiB	15 days, 22 hours
IGA	356 TiB	316 TiB	52 days, 7 hours

The relatively low uptime percent for the initial calculation is a result of a 1 week pause in the calculation to make the laptop available for other purposes (midterms).

I believe the first method (Vidunas–Lamprecht) is intrinsically more efficient than the Incomplete Gamma Approximation; however, most of the observed performance gap is due to hardware differences. The laptop had an NVMe SSD and a much newer CPU compared to the older hard drives and processor in the Debian server used for verification.

Over the two runs combined, more than 1.6 Pebibytes (PiB) of data (about $1.64 \cdot 10^6$ GiB) as read and written to disk. No I/O errors were detected, and all drives remain in full working condition.

Results

Here are the last digits I computed (numbered 174,999,999,901 to 175,000,000,000), broken into groups of 10 for clarity:

6180267994 6874068253 4568233834 0586791383 1778803247 0727912102 7020053472 8225828190 3835497822 1028929467

Aftermath

When I started this computation, the record for Gamma(1/5) (completed by Dmitriy Grigoryev) was 135 billion decimal digits, announced on February 20, 2025; however, a new computation of 220 billion digits was completed on May 26, 2025- 5 days before I completed my 175 billion digit computation.

However, this was still a fun personal challenge that provided interesting results on the computation time comparison between a modern laptop and an older server for I/O-bound calculations.